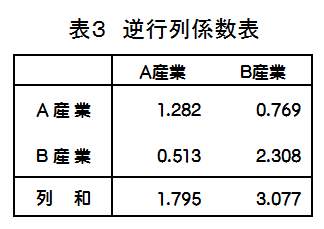
産業連関表では、タテ方向の計数の並びを「列」といいます。各列では、その部門の財・サービスの生産に当たって用いられた原材料、燃料、労働力などへの支払の内訳(費用構成)が示されており、産業連関表では、これを「投入」(input)といいます。
一方、ヨコ方向の計数の並びを「行」といいます。各行では、その部門で生産された財・サービスの販売先の内訳(販路構成)が示されており、産業連関表では、これを「産出」(output)といいます。
このため、産業連関表は、「投入産出表」(Input-Output Tables、略してI−O表)とも呼ばれています。
「産業連関表」として作成される統計表には、様々なものがありますが、その中核となるのが「取引基本表」であり、他の統計表は、取引基本表に基づいて作成されています。そのため、取引基本表を指して「産業連関表」と呼称することもあります(図1は、取引基本表の概念図を示したものとなります。)。
そこで、ここでは、取引基本表と主要係数表である投入係数表及び逆行列係数表の関係について、具体的な数値例で説明します。
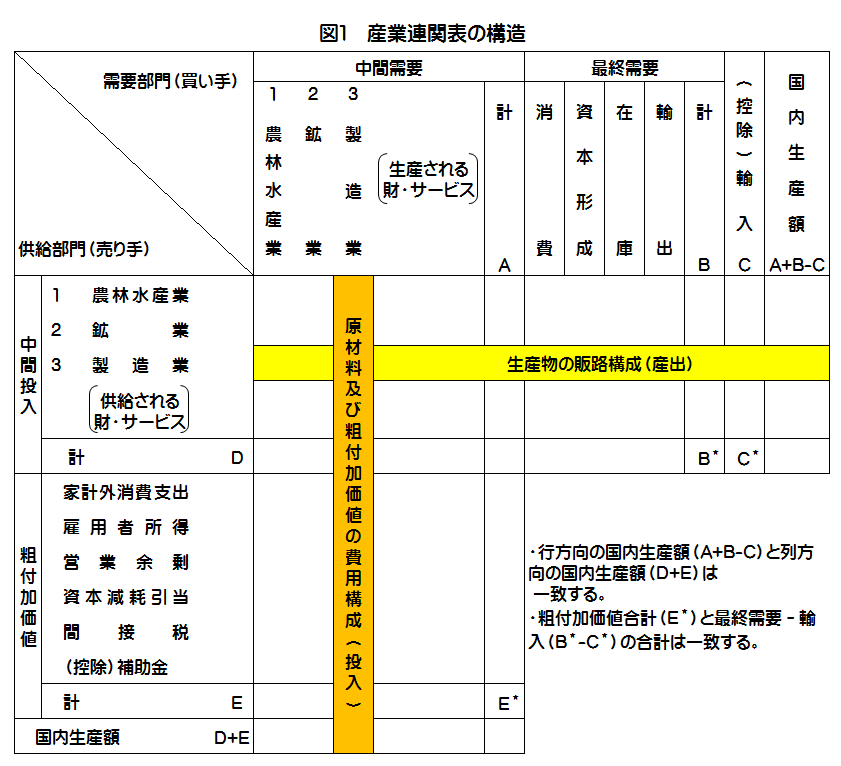
「取引基本表」は、産業相互間や産業と最終需要(家計など)との間で取引された財・サービスの金額を行列形式で表示したものです。
例えば、表1の場合、A産業をタテ(列)に見ると、原材料等の中間投入としてA産業から30億円、B産業から60億円購入し、210億円の粗付加価値が加わることで300億円の生産が行われたことを示しています。一方、A産業をヨコ(行)に見ると、生産額300億円のうち、中間需要としてA産業に30億円、B産業に150億円販売(産出)され、残る120億円が最終需要として販売されたことを示しています。
なお、取引基本表は、各部門とも、タテの合計(投入額合計)とヨコの合計(産出額合計)が一致するように作成しています。表1では、A産業については300億円、B産業については500億円で、タテ・ヨコともに一致していることがわかります。
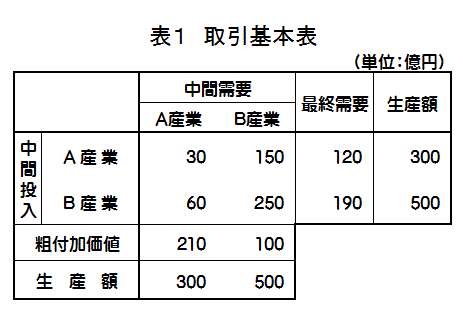
「投入係数」とは、取引基本表の中間需要の列部門ごとに、原材料等の投入額を当該部門の生産額で除して得た係数のことをいいます。例えば、表1のA産業について投入係数を求めると、各投入額をA産業の生産額300億円で除したものとなり、表2のとおり、A産業が0.1、B産業が0.2、粗付加価値が0.7となります。
つまり、投入係数とは、ある産業において1単位の生産を行う際に必要とされる原材料等の単位を示したものであり、これを使用することにより、取引基本表では金額で表されている産業間の取引関係を比率として見ることが可能になります。そして、この投入係数を列部門別に一覧表にしたものが「投入係数表」であり、表1から算出される投入係数表は、表2のようなものとなります。
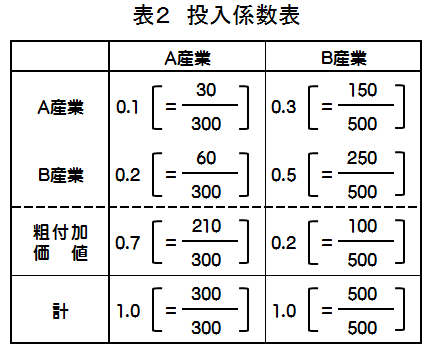
「逆行列係数」とは、ある部門に対して新たな最終需要(以下「新規需要」といいます。)が1単位発生した場合に、当該部門の生産のために必要とされる(中間投入される)財・サービスの需要を通して、各部門の生産がどれだけ発生するか、つまり、直接・間接の生産波及の大きさを示す係数であり、その算出方法を踏まえ、数学上の用語を用いて、このように呼称されています。
例えば、図2のとおり、A産業で生産する財・サービスに新規需要が1単位発生した場合、A産業の生産そのものを1単位増加させる必要があることは言うまでもありませんが(直接効果)、そのためにはA産業における生産活動で用いられる原材料の投入を増加させる必要があり、A産業には0.1、B産業には0.2の生産増が発生します(間接効果(第1次))。そして、このA産業0.1及びB産業0.2の生産増のために用いられる原材料について、更なる生産の増加が必要となり(間接効果(第2次))、このような投入係数を介した波及が続いていくことになります。そして、この究極的な大きさの総和が逆行列係数に相当し、これを産業別に一覧表にしたものが「逆行列係数表」(表3)となります。
このように、逆行列係数表は、特定部門の生産を1単位行うために、直接・間接に必要とされる各部門の生産増加の水準が、最終的にどのくらいになるかを算出した表であることから、この表の列和は、当該部門に新規需要が1単位発生したときの産業全体への波及効果の合計に相当します。表3の例でいえば、A産業に新規需要が1単位発生した場合、産業全体で1.795の波及効果を生じさせることを表していることになります。